Die vorliegenden 47 Kopiervorlagen enthalten Arbeitsblätter zu wesentlichen inhaltlichen Schwerpunkten bei der Behandlung von Funktionen. Ein Einsatz dieser Arbeitsblätter ist sowohl bei der Behandlung der entsprechenden Sachverhalte im Mathematikunterricht der
Sekundarstufe I in verschiedenen Klassenstufen und Schultypen als auch in
Arbeitsgemeinschaften möglich.

Die Aufgaben der Kopiervorlagen sind innerhalb der einzelnen Abschnitte nicht nach
Anforderungsniveau, sondern nach dem Inhalt geordnet. Einige enthalten mehrere
Teilaufgaben und verlangen von den Schülerinnen und Schülern eine höhere Komplexität in der Bearbeitung eines Sachverhalts. Die meisten Teilaufgaben können aber auch einzeln gelöst werden.

Lehrerinnen und Lehrer können aus einem vielfältigen Angebot an Aufgaben (z. B. Aufgaben unterschiedlichen inhaltlichen Niveaus, einfache und komplexe Aufgaben) geeignete
Beispiele für ein differenziertes Lernen, für variantenreiches Festigen und Anwenden, für das Ermitteln von Schülerleistungen bzw. auch für mündliche und schriftliche Kontrollen
auswählen.

Auf der Rückseite eines jeden Arbeitsblattes sind jeweils die von den Schülerinnen und Schülern zu erwartenden Lösungen angegeben. Jenes knappe Erwartungsbild mit
Beispielcharakter dient vorrangig zur Information der Unterrichtenden.

Durch die Kopiervorlagen sollen Lehrerinnen und Lehrer sowohl Hilfe und Unterstützung als auch Anregungen für die Gestaltung ihres Unterrichts erhalten. So können die Arbeitsblätter beispielsweise als Grundlage für die Zusammenstellung von Aufgaben für mündliche und schriftliche Leistungskontrollen im Fach Mathematik sowie zur langfristigen Vorbereitung auf Prüfungen dienen. Auch lassen sie sich parallel zum laufenden Unterricht nutzen,
insbesondere als Ergänzung zum Aufgabenangebot in Lehrbüchern und methodischen Handreichungen.

Im Unterricht selbst ist ein Einsatz der Arbeitsblätter zur Wiederholung und Systematisierung des mathematischen Stoffes, aber auch zur Leistungsüberprüfung möglich. Durch das
differenzierte Angebot einer Vielzahl von Aufgaben unterschiedlichen Typs können sie zur gezielten Entwicklung von Kompetenzen innerhalb eines handlungsorientierten und
schüleraktiven Mathematikunterrichts beitragen. Die Verwendung solcher Operatoren wie Beschreibe, Begründe, Erkläre, De?niere, Bewerte, Vergleiche, Erläutere oder Interpretiere unterstützt diesen Prozess.

Inhaltsverzeichnis:

Zuordnungen

• Blatt 1: Proportionale Zuordnungen
• Blatt 2: Antiproportionale Zuordnungen
• Blatt 3: Gemixtes zu Zuordnungen

Lineare Funktionen

• Blatt 4: Funktionen mit Gleichungen der Form y = m·x
• Blatt 5: Graphen zeichnen und Anstieg ermitteln
• Blatt 6: Funktionen mit Gleichungen der Form y = m·x + n
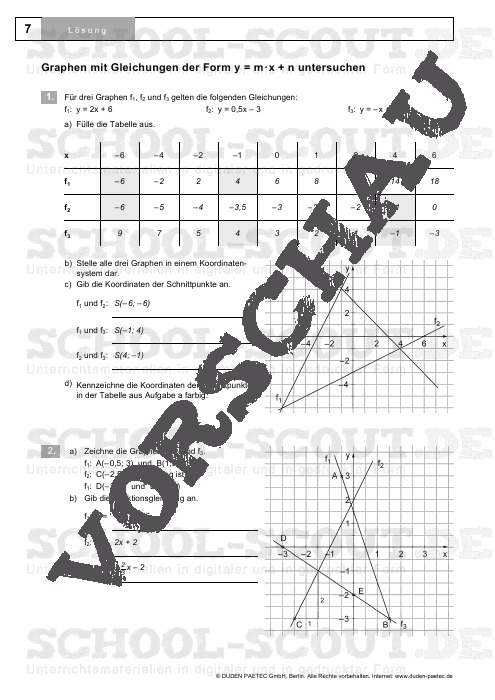
• Blatt 7: Untersuchen von Graphen mit Gleichungen der Form y = m·x + n
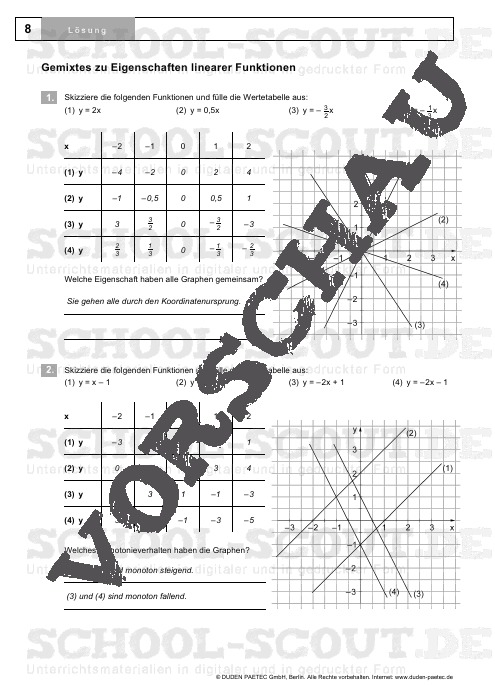
• Blatt 8: Gemixtes zu Eigenschaften linearer Funktionen
• Blatt 9: Gemixtes zur Anwendung linearer Funktionen
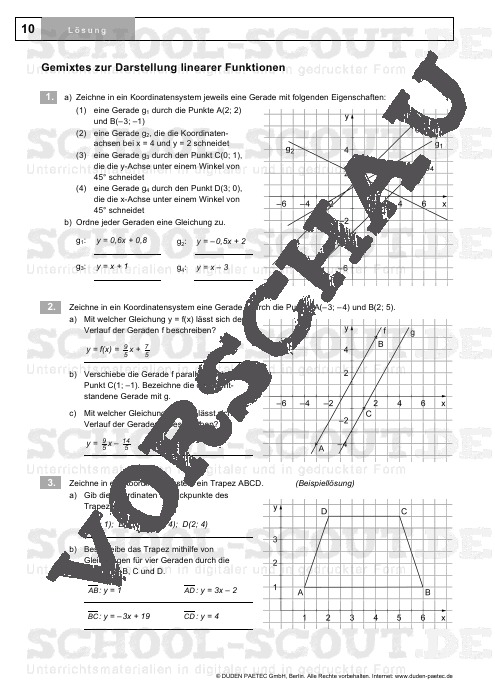
• Blatt 10: Gemixtes zur Darstellung linearer Funktionen

Quadratische Funktionen:

• Blatt 11: Die quadratische Funktion mit der Gleichung y =
• Blatt 12: Einfluss des Faktors a auf den Verlauf der Graphen der Funktion y = a·x2
• Blatt 13: Stauchung, Streckung, Spiegelung von Graphen
• Blatt 14: Funktionen mit Gleichungen der Form y = x2 + e
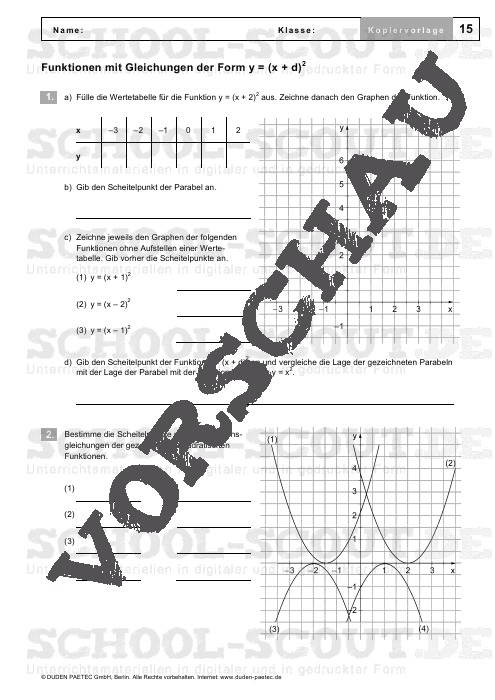
• Blatt 15: Funktionen mit Gleichungen der Form y = (x + d)2
• Blatt 16: Funktionen mit Gleichungen der Form y = (x + d)2 + e und y = x2 + p·x + q
• Blatt 17: Scheitelpunktsform, Normalform, Nullstellen
• Blatt 18: Schnittpunkt zweier Parabeln bestimmen
• Blatt 19: Einfluss des Faktors a auf den Verlauf der Graphen
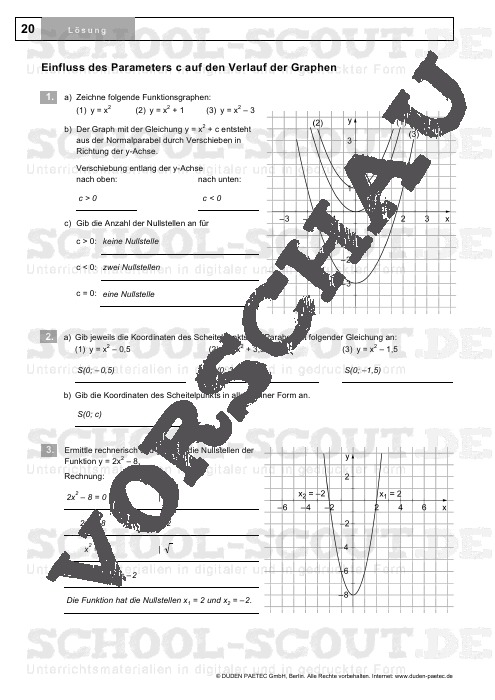
• Blatt 20: Einfluss des Parameters c auf den Verlauf der Graphen
• Blatt 21: Einfluss der Parameter d und e auf den Verlauf der Graphen
• Blatt 22: Gemixtes zu Funktionen mit Gleichungen der Form y = x2 + p·x + q
• Blatt 23: Gemixtes zu Berechnungen von Schnittpunkten

Potenzfunktionen und Wurzelfunktionen

• Blatt 24: Funktionen mit Gleichungen der Form y = x2n mit n > 0
• Blatt 25: Funktionen mit Gleichungen der Form y = x2n mit n < 0
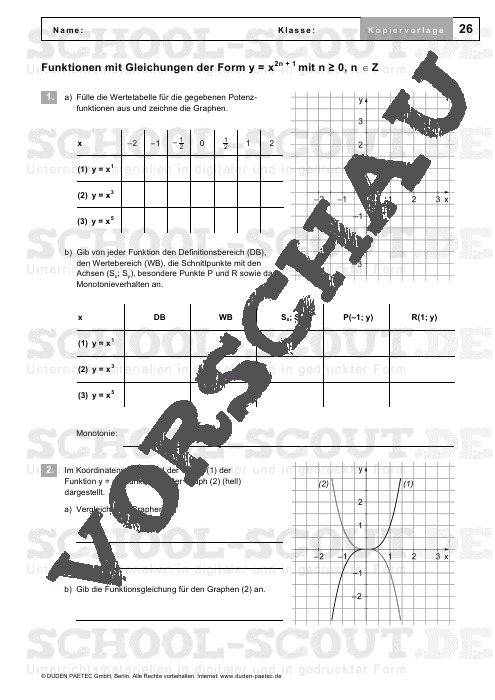
• Blatt 26: Funktionen mit Gleichungen der Form y = x2n + 1 mit n > 0
• Blatt 27: Funktionen mit Gleichungen der Form y = x2n + 1 mit n < 0
• Blatt 28: Funktionen mit Gleichungen der Form
• Blatt 29: Potenzfunktionen mit der Gleichung y = x2n (Systematisierung)
• Blatt 30: Potenzfunktionen mit der Gleichung y = x2n + 1 (Systematisierung)
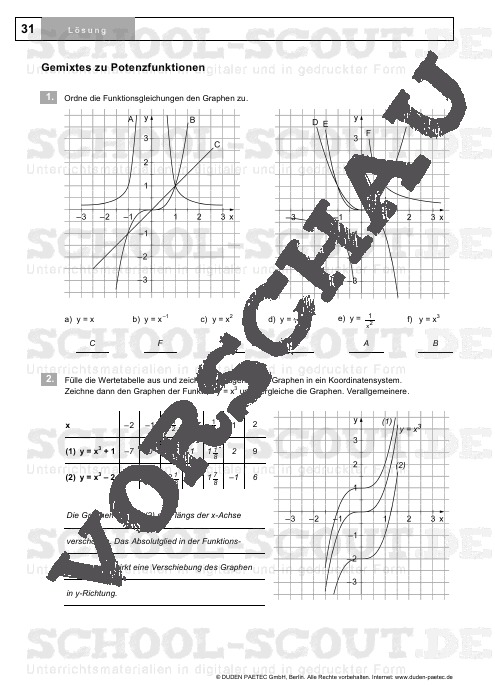
• Blatt 31: Gemixtes zu Potenzfunktionen
• Blatt 32: Gemixtes zum Verlauf von Graphen^

Exponentialfunktionen

• Blatt 33: Funktionen mit der Gleichung y = ax
• Blatt 34: Einfluss des Faktors k auf den Verlauf der Graphen der Funktion y = k·ax
• Blatt 35: Wachstum und Zerfall
• Blatt 36: Gemixtes zur Bestimmung von Funktionsgleichungen
• Blatt 37: Gemixtes zur Darstellung von Funktionen

Winkelfunktionen

• Blatt 38: Gradmaß und Bogenmaß
• Blatt 39: Funktionen mit der Gleichung der Form y = sinx und y = a·sinx
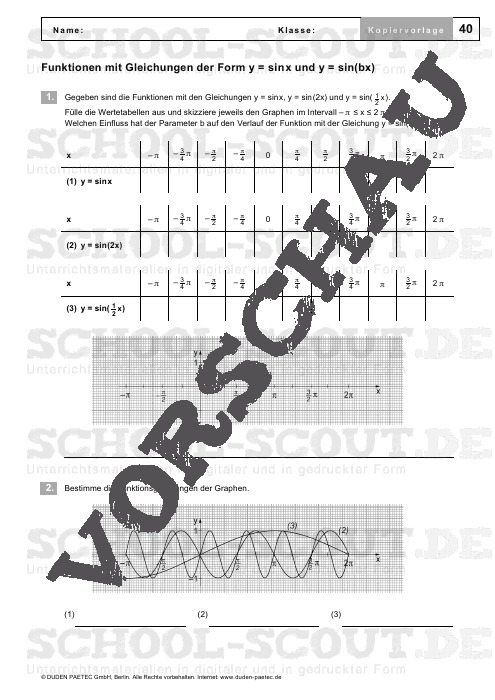
• Blatt 40: Funktionen mit Gleichungen der Form y = sinx und y = sin(bx)
• Blatt 41: Funktionen mit der Gleichung der Form y = sinx, y = a·sinx und y = sin(bx)
• Blatt 42: Funktionen mit Gleichungen der Form y = cosx
• Blatt 43: Ermitteln von Winkelgrößen und Kosinuswerten
• Blatt 44: Funktionen mit Gleichungen der Form y = tanx
• Blatt 45: Gemixtes zu Winkelfunktionen
• Blatt 46: Gemixtes zu trigonometrischen Berechnungen

Teste dein Wissen

• Blatt 47: MC-Test zu Funktionen