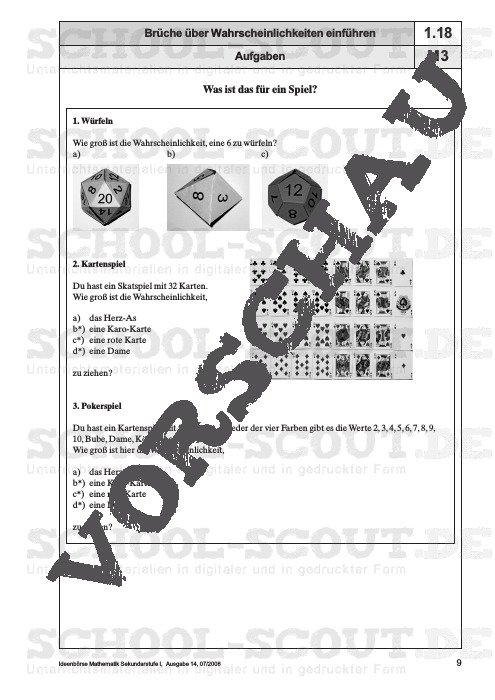
Brüche über Wahrscheinlichkeiten einführen
Bruchrechnung und Wahrscheinlichkeit nach den Bildungsstandards
- Typ:
- Unterrichtseinheit
- Umfang:
- 19 Seiten (0,5 MB)
- Verlag:
- Mediengruppe Oberfranken
- Fächer:
- Mathematik
- Klassen:
- 5-6
- Schulform:
- Gymnasium, Hauptschule, Realschule
Bruchrechnung in Klasse 5 und 6: In den neuen Bildungsstandards spielt die Wahrscheinlichkeitsrechnung in jeder Stufe eine große Rolle. Warum also nicht Bruchrechnung und Wahrscheinlichkeit kombinieren? Das Besondere an diesen Ausführungen ist nicht die Idee der Kombination der beiden Themen, denn diese ist von Natur aus vorgegeben, außergewöhnlich ist, dass die Bruchrechnung mit den Ideen der Wahrscheinlichkeitsrechnung eingeführt wird.
Kompetenzen und Unterrichtsinhalte:
- Die Schüler lernen elementare Regeln und Gesetze des Bruchrechnens und der Wahrscheinlichkeitsrechnung kennen und anwenden. * Die Schüler lernen und experimentieren binnendifferenziert.
- Sie setzen sich mit verschiedenen Glücksspielen und der Spielsucht auseinander.
- Sie gestalten ein eigenes Spielcasino z.B. als Beitrag für ein Schulfest.
Bei gemeinsamem Entdecken, Erforschen, Beschreiben und Erklären von mathematischen Vorstellungen soll das Bruchrechnen über die Betrachtung von Wahrscheinlichkeiten eingeführt werden. An erster Stelle steht dabei die Motivation, die die Schüler zum einen durch das Thema, zum anderen durch die Vorfreude auf das anstehende Projekt einer „Spielhölle“ erhalten und auch aufrecht halten können. Die Gestaltung des Unterrichts ermöglicht den Schülern zahlreiche und vielfältige Erfahrungen, welche sie dazu anregen und befähigen sollen, mathematische Denkweisen zu entwickeln und die Bedeutung der Bruch- und Wahrscheinlichkeitsrechnung zu verstehen und vielleicht sogar zu schätzen. Zudem besteht die Möglichkeit, innerhalb der Übungsphasen zu differenzieren.
Die folgenden Seiten sollen Ideengeber und ein roter Faden durch das Thema sein; sie erheben keineswegs den Anspruch auf Vollständigkeit. Weiteren Ideen und Ausweitungen sind keine Grenzen gesetzt. Der bessere Unterricht entsteht immer erst durch die eigene Verarbeitung der Anregungen anderer Kollegen.