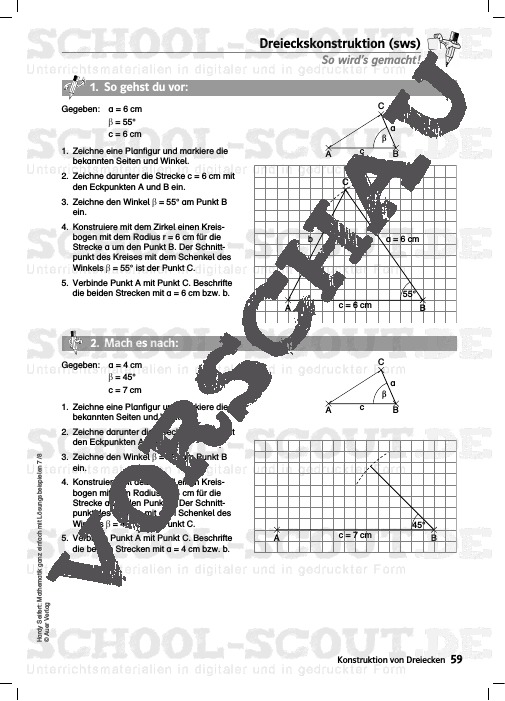
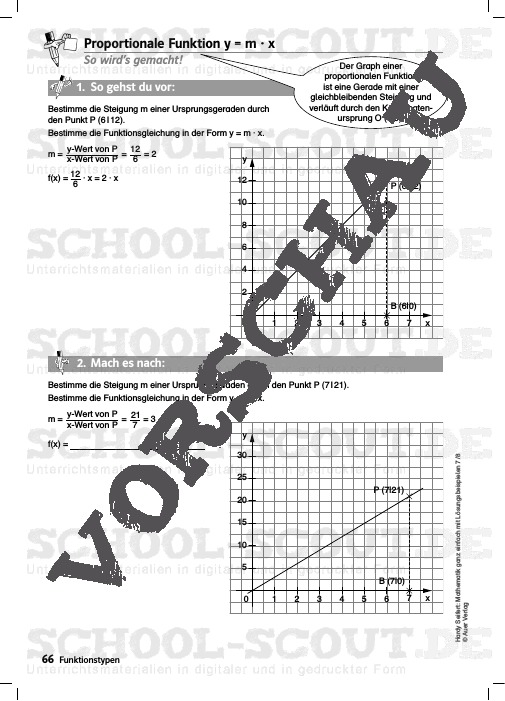
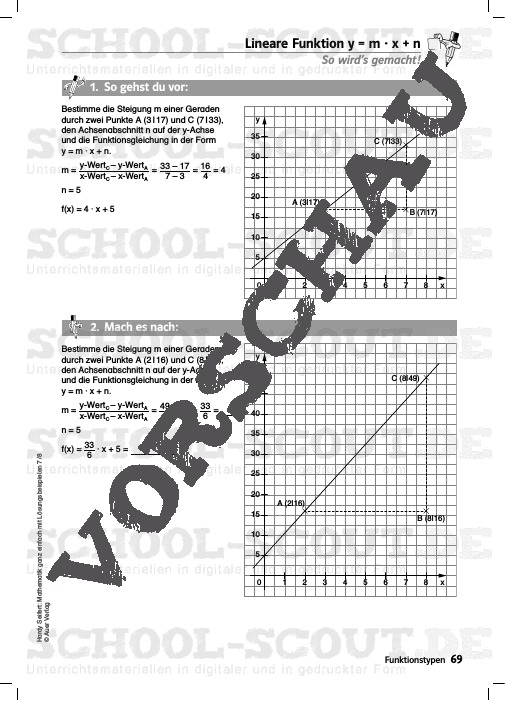
In dieser Unterrichtshilfe werden zu jedem Thema zwei Arbeitsblätter angeboten: Auf dem ersten Arbeitsblatt mit dem Titel „So wird’s gemacht!“, finden die Schüler die Lösungsbeispiele, wobei nur das erste Beispiel („1 . So gehst du vor“) komplett ausgearbeitet ist. Die nächsten beiden Aufgaben („2 . Mach es nach“, „3 . Jetzt wird es schwieriger“) sind Teillösungen, die die Lernenden nach dem Muster des ersten Beispiels zu einer Lösung ergänzen müssen. Dabei erhöht sich sukzessive die Komplexität bis zur letzten Aufgabe („4 . Jetzt kannst du es“).

Das zweite Arbeitsblatt mit dem Titel „Geh der Sache auf den Grund!“ leitet die Lernenden mit abwechslungsreichen Aufgabenstellungen dazu an, sich nochmals mit den einzelnen Schritten in den Beispielen auseinanderzusetzen und diese zu reflektieren. Dabei entstehen Selbsterklärungen, die zu einem tieferen Verständnis für die Vorgehensweise in den Beispielen führen sollen.

Die Lösungen finden sich am Ende des Heftes .

Inhaltsverzeichnis

Klasse 7

• Zuordnung
  • Proportional
  • Antiproportional
• Mit ganzen und rationalen Zahlen rechnen
  • Addition
  • Subtraktion
  • Multiplikation
  • Division
• Winkel
  • Winkel an sich schneidenden Geraden
• Besondere Linien im Dreieck
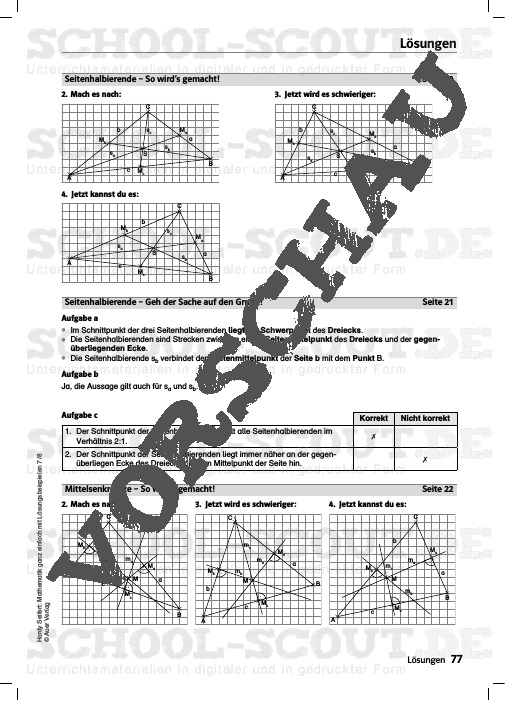
  • Seitenhalbierende
  • Mittelsenkrechte
  • Höhen
  • Winkelhalbierende
• Prozentrechnung
  • Prozentwert
  • Prozentsatz
  • Grundwert
• Terme und Gleichungen
  • Terme
  • Lineare Gleichung

Klasse 8

• Terme berechnen
  • Ausklammern
  • Klammer mal Klammer
  • 1 . Und 2 . Binomische Formel
  • Binomische Formel
• Prozentrechnung
  • Verminderter Grundwert
  • Vermehrter Grundwert
• Zinsrechnung
  • Kapital
  • Zinsen
  • Zinssatz
• Konstruktion von Dreiecken
  • Dreieckskonstruktion (sss)
  • Dreieckskonstruktion (sws)
• Ebene Figuren
  • Flächeninhalt Dreieck
  • Flächeninhalt Trapez
• Funktionstypen
  • Proportionale Funktion y = m · x
  • Lineare Funktion y = m · x + n

Lösungen