Im Bildungsplan des Landes Baden-Württemberg wie auch der anderen Bundesländer wird als Ziel des Kompetenzerwerbes für den mittleren Abschluss unter anderem gefordert: „Ich kann quadratische Gleichungen und lineare Gleichungssysteme sowie Bruch- und Potenzgleichungen lösen“. Wie im Jahr 2018 gibt es in den meisten Jahren bei den Prüfungsaufgaben zum Realschulabschluss in Baden-Württemberg eine Aufgabe zum Lösen einer anspruchsvollen Bruchgleichung, wie auch das Titelbild dieses Heftes verrät.

Im Schulalltag lautet hingegen die widerspenstige Antwort vieler Schüler auf die oben geforderte Kompetenz „Wozu braucht man denn das…?“. Wir kennen alle die Zweifel der Schüler an der Notwendigkeit Bruchgleichungen lösen zu müssen – geboren aus den Schwierigkeiten beim Umgang mit diesem Typ von Gleichungen. Und obwohl die Schüler dieses Stoffgebiet gerne umgehen möchten, sind wir Lehrer um so mehr gefordert, speziell bei der Behandlung der Bruchgleichungen zu zeigen, wie man mit dem Werkzeug bekannten Wissens sowie mit Sorgfalt und Ausdauer diese Gleichungen lösen kann.

Zum Motivieren unter dem Vorsatz, dass Bruchgleichungen benötigt werden, um Sachverhalte aus Naturwissenschaft und Technik mathematisch zu modellieren bzw. mit Hilfe von entsprechenden Formeln gesuchte Größen zu ermitteln sowie beim Erlangen von Fertigkeiten beim Lösen dieser Gleichungen, kann der Einsatz vorliegender Arbeitsmaterialien hilfreich sein.

Auf den ersten Seiten soll den Schülern anhand einer Auswahl von repräsentativen Aufgaben wie zum Beispiel einer historischen Aufgabe des Heron von Alexandria und Zahlenrätseln sowie einem Überblick über die Schwerpunkte beim Lösen von Bruchgleichungen ein Eindruck davon vermittelt werden, worum es in diesem Stoffgebiet geht.

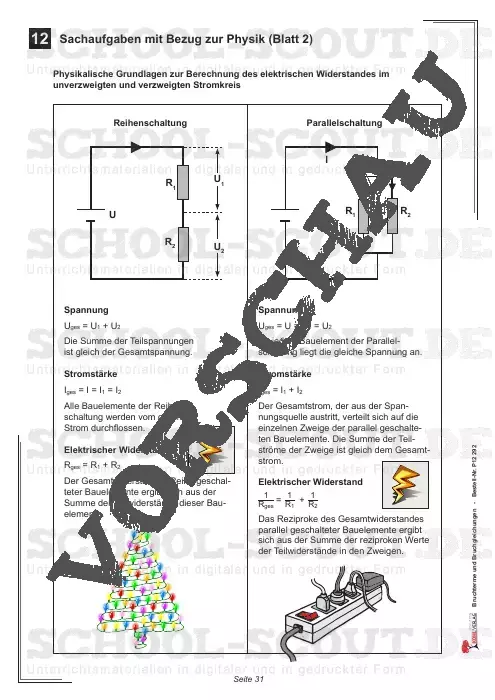
Als Bruchgleichungen sind ja bekanntlich solche Gleichungen definiert, bei welchen die Variable mindestens einmal im Nenner der Bruchterme, aus welchen sich die Bruchgleichungen zusammensetzen, vorkommt. Daraus folgt, dass bei der Belegung der Variablen einige Zahlen ausgeschlossen werden müssen, da Division durch Null nicht möglich ist. Eine Vielzahl von Aufgaben fordert deshalb die Bestimmung des Definitionsbereiches von Bruchtermen und Bruchgleichungen – der Menge der für die Belegung der Variablen zugelassenen Zahlen.

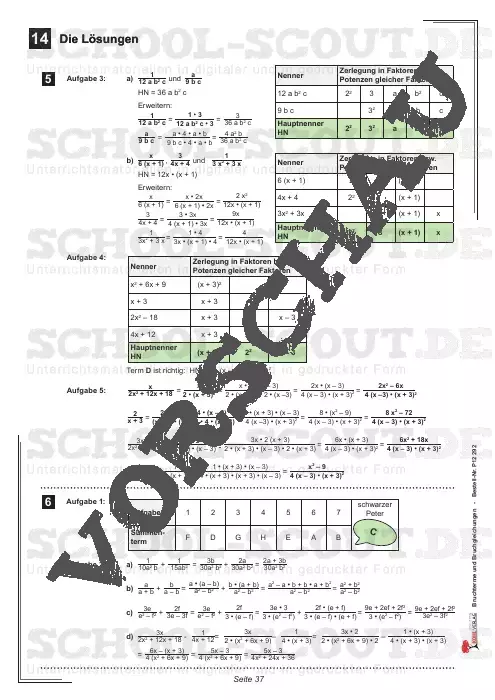
Zum Handwerkszeug beim Lösen von Bruchgleichungen gehören insbesondere auch Kenntnisse und Fähigkeiten beim Ermitteln des Hauptnenners als kleinstes gemeinsames Vielfaches der auftretenden Nenner, Faktorisieren von Summen sowie Gleichnamigmachen und Erweitern von Brüchen – wobei alles, was für Brüche gilt, nun auf Bruchterme übertragen werden muss.

Deshalb werden in diesem Arbeitsheft zahlreiche Aufgaben zur „Kleinarbeit“ mit Termen vorangestellt, bevor es an das Lösen von Bruchgleichungen mit aufsteigendem Schwierigkeitsgrad geht. Die entsprechenden Seiten dazu bilden den Schwerpunkt des Heftes. Hier gibt es Aufgaben – angefangen von den einfachsten Formen bis hin zu Bruchgleichungen, die nach dem Umformen zu quadratischen Gleichungen führen – mit Orientierung an den entsprechenden Aufgaben zum Realschulabschluss in Baden-Württemberg.

Dabei werden die Schüler mit ausführlich erläuterten Beispielen und Lösungshilfen an das selbstständige Lösen dieser Aufgaben herangeführt.

Sachaufgaben zu physikalischen Anwendungen im letzten Kapitel und „Röhrenaufgaben“– wie schon zu Herons Zeiten bekannt – sollen dazu beitragen, den Schülern bewusst zu machen, dass Bruchgleichungen in der Praxis gelöst werden müssen und runden unter fachübergreifendem Aspekt das Thema Bruchgleichungen ab.

Inhaltsverzeichnis:

• Worum es geht?
  • Eine Aufgabe zur Einführung
  • Zahlenrätsel als Beispiel
  • „Auf einen Nenner gebracht“
• Was sind Bruchgleichungen und welche Schwerpunkte sind beim Lösen zu beachten?
• Definitionsbereich von Bruchtermen/-gleichungen bestimmen (Blatt 1 bis Blatt 3)
• Zur Wiederholung ein kleiner Exkurs in die Bruchrechnung
• Hauptnenner von Bruchtermen und Bruchgleichungen (Blatt 1 bis Blatt 3)
• Addieren und Subtrahieren von Bruchtermen
• Bruchgleichungen der einfachsten Form lösen (Blatt 1 bis Blatt 3)
• Gleichungen mit Summen von Bruchtermen (Blatt 1 bis Blatt 4)
• Bruchgleichungen, die auf quadratische Gleichungen führen (Blatt 1 bis Blatt 5)
• Zahlenrätsel 28 Schnittpunkt von Funktionsgraphen
• Sachaufgaben mit Bezug zur Physik (Blatt 1 bis Blatt 3)
• Herons Brunnen heute
• Die Lösungen