Unendlichkeit in der Mathematik - Rechnen mit Unendlichkeit
Von unendlich groß bis unendlich klein - endlich spannend erklärt!
- Typ:
- Unterrichtseinheit
- Umfang:
- 68 Seiten (15,7 MB)
- Verlag:
- Kohl Verlag
- Autor/in:
- Theuer, Barbara
- Auflage:
- 2 (2020)
- Fächer:
- Mathematik
- Klassen:
- 9-13
- Schulform:
- Gymnasium, Realschule
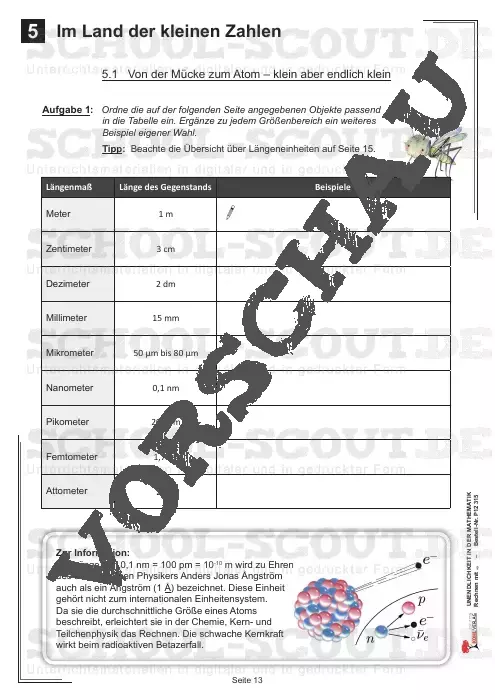
Ausgehend von der Erfahrungswelt der Schüler wie beispielsweise der Frage nach der Zahl der Körner in einer Sanduhr oder dem Brauch des „Schafe zählens“ vor dem Einschlafen bis hin zu Fragen nach der Unendlichkeit des Kosmos und der Teilbarkeit der Körper finden sich auf den ersten Seiten dieser Unterrichtseinheit Texte, Aufgaben und Rätsel zur allgemeinen Problematik der Unendlichkeit.
Die Schüler werden weiterhin mit Beispielen für sehr große – aber endlich große – und sehr kleine – aber endlich kleine – Größen und Zahlen bekanntgemacht und mit Beispielen dafür sensibilisiert, dass man unter „Unendlich groß“ keine Zahl, sondern einen Prozess „des immer weiter Zählens“ und unter „Unendlich klein“ einen Prozess „des immer weiter Teilens“ verstehen kann.
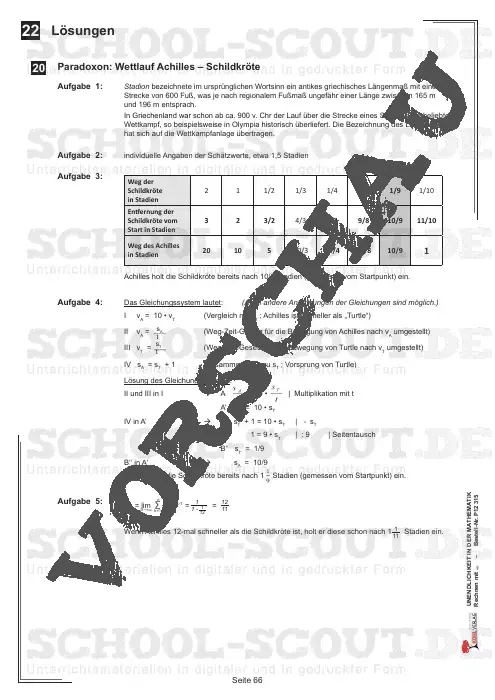
Ein Blick in die Geschichte der Mathematik zeigt den Schülern, dass sich Forscher seit der Antike mit der Problematik des Unendlichen beschäftigten. Ausführlich wird Zenons Paradoxon von Achilles und der Schildkröte vorgestellt.
Den Schwerpunkt des Heftes bilden vielfältige Aufgaben zu Zahlen- und Partialsummenfolgen (Reihen) beginnend mit Zahlenreihen, in welchen fehlende Zahlen zu ergänzen sind.
Rätsel oder die Suche nach einem Bildungsgesetz kommen als Strategien zum Lösen der Aufgaben infrage. Historische Beispiele wie die Fibonacci-Folge und die Legende von der Erfindung des Schachspieles sind mit Texten und entsprechenden Aufgaben eingebunden. Interessant wird es dann, wenn endlos viele Folgenglieder addiert werden und dennoch die Summe einen endlichen Wert – den Grenzwert – nicht überschreitet.
Der Ausblick auf das Rechnen mit unendlich kleinen Größen, was in der Antike nicht
gelang, aber seit dem Wirken von Leibnitz und Newton, die als Begründer der Infinitesimalrechnung gelten, möglich wurde, rundet das Material ab, welches sowohl zur Ergänzung im Unterricht der Mittelstufe, in Freiarbeit, zur Vorbereitung auf die Einführung der Analysis in der Oberstufe oder aber auch als häusliche Lektüre für interessierte Schüler eingesetzt werden kann.