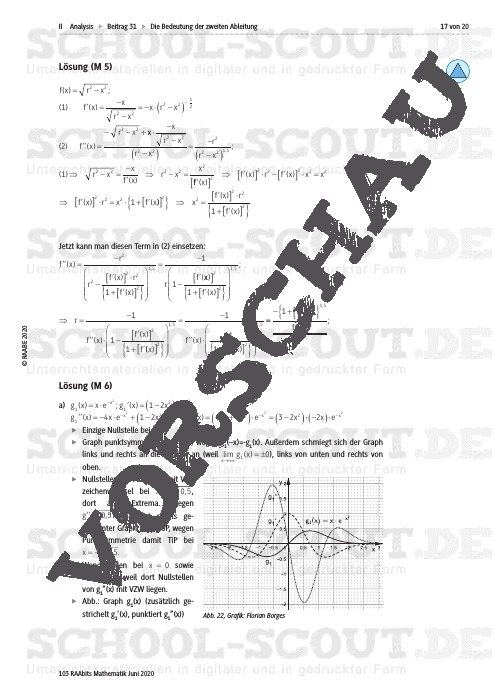
Funktionale Zusammenhänge zwischen zwei Zahlenbereichen (üblicherweise x und y = f(x)) werden gern als Graphen dargestellt, deren Steigungsverhalten sich in vielfältiger Weise ändern kann. Der Graph kann steigen, dann immer stärker steigen oder immer weniger stark. Entsprechendes gilt für das Fallen. Analytisch wird dieses grafische Verhalten beschrieben durch die 1. bzw. 2. Ableitung und insbesondere deren Vorzeichen bzw. Nullstellen. Haben die Schüler die Ankeridee der 1. Ableitung verstanden, stellt auch der Transfer auf die Ableitung der Ableitung bzw. die 2. Ableitung kein großes Problem mehr dar.

KOMPETENZPROFIL:

• Klassenstufe: 11/12 (G9)
• Dauer: 6–8 Unterrichtsstunden
• Kompetenzen: Mathematisch argumentieren (K1), Probleme mathematisch lösen (K2), Mathematisch modellieren (K3), Mathematische Darstellungen verwenden (K4), Kommunizieren (K5)
• Thematische Bereiche: Differenzialrechnung
• Zusatzmaterialien: GeoGebra-Dateien