Wirft man eine „ideale“ Münze n-mal und betrachtet das Ergebnis „Wappen“ als Treffer, so geht man davon aus, dass die Trefferwahrscheinlichkeit p = 0,5 ist.
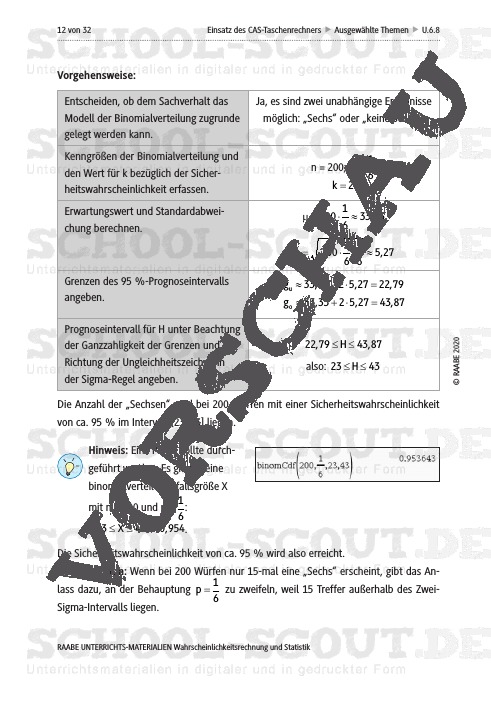
Trotzdem wird es in einer konkreten Stichprobe des Umfangs n häufig passieren, dass nicht genau die Hälfte der Ergebnisse „Wappen“ lautet. Vielmehr wird man erwarten dürfen, dass die Anzahl der Treffer zufallsbedingt in einem Intervall um den Erwartungswert liegt. Im Mathematikunterricht der Oberstufe lassen sich solche Prognoseintervalle im Zusammenhang mit den Sigma-Regeln der Binomialverteilung quantitativ berechnen und inhaltlich interpretieren. Sie bieten einen sehr guten Zugang zur Betrachtung von Konfidenzintervallen.

Inhaltsverzeichnis:

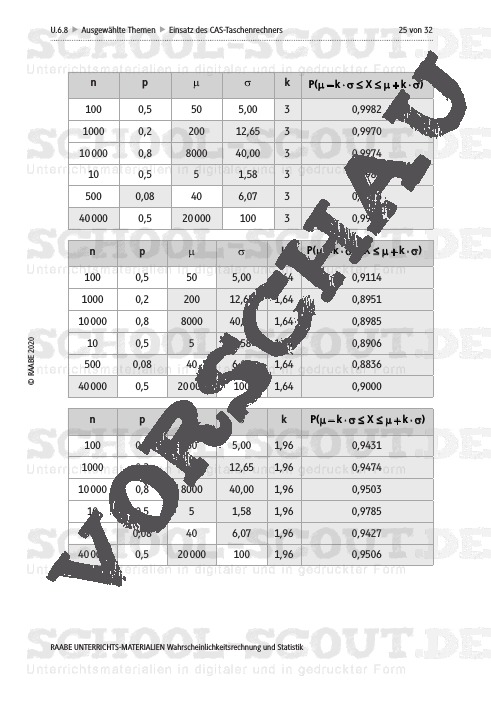
• M 1 Die Sigma-Regeln der Binomialverteilung
• M 2 Hypergeometrische Verteilung/Binomialverteilung
• M 3 Prognoseintervalle für absolute Häufigkeiten
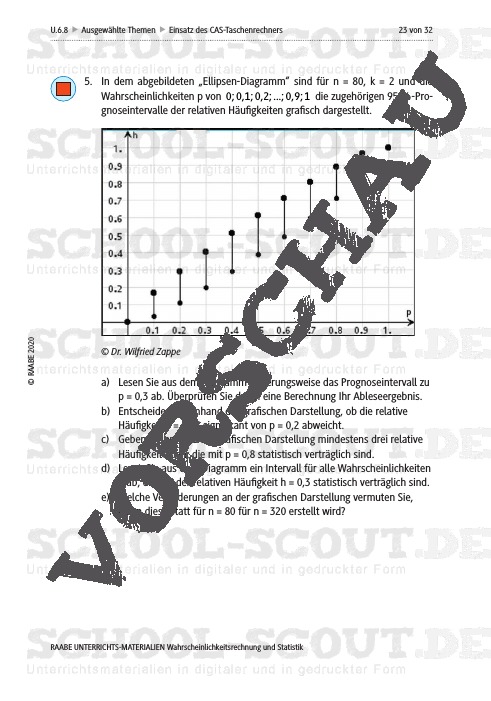
• M 4 Prognoseintervalle für relative Häufigkeiten
• Lösungen

Die Schüler lernen:

• die Sigma-Regeln für binomialverteilte Zufallsgrößen anzuwenden,
• Prognoseintervalle für absolute und relative Häufigkeiten bei Stichproben binomial-verteilter Zufallsgrößen zu berechnen und zu interpretieren,
• die Begriffe „signifikante Abweichung“ und „statistische Verträglichkeit“ sachgerecht zu verwenden,
• die Möglichkeit der Näherung hypergeometrisch verteilter Zufallsgrößen durch binomialverteilte Zufallsgrößen kennen und anzuwenden,
• die Möglichkeiten des CAS-Rechners zur Berechnung und Visualisierung von Prognoseintervallen auszunutzen.