Extremwertprobleme und Anwendungen bei einer Exponentialfunktion gehören zu den Standardaufgaben des Analysis-Unterrichts der Oberstufe.

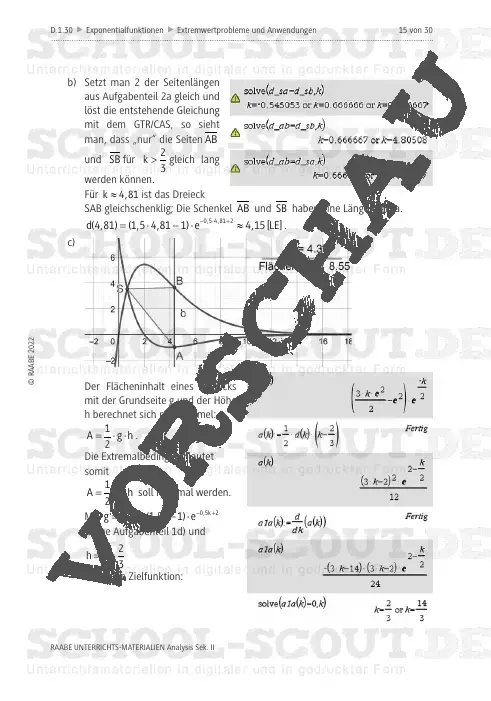
Nimmt man jedoch zum Graph einer Funktion noch z. B. den Graphen der Ableitungsfunktion oder den verschobenen bzw. gespiegelten Graphen der Funktion hinzu, so lassen sich dazwischen Dreiecke mit bestimmten Eigenschaften legen. Ebenso können Figuren zwischen die Graphen gelegt werden, sodass der Flächeninhalt maximal wird. Die Funktionsuntersuchung erweitert der Beitrag damit um Extremalwertaufgaben. Der Graph einer Exponentialfunktion und der gespiegelte bzw. verschobene Graph der Funktion bilden bei weiteren Aufgaben den Querschnitt von Körpern. Anwendungsaufgaben stellen bestimmte Anforderungen an diese Körper, welche die Lernenden lösen.

Die Schüler und Schülerinnen lernen:

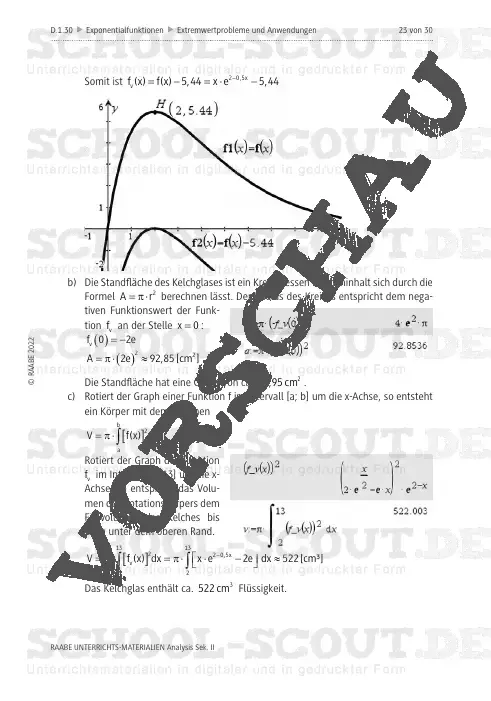
durch Ableitung einer Exponentialfunktion oder Spiegelung bzw. Verschiebung ihres Graphen weitere Graphen zu bestimmen. Sie legen zwischen die Graphen ein Dreieck, welches abhängig von einer Parallelen zur y-Achse rechtwinklig oder gleichschenklig sein kann. Ebenso legen die Jugendlichen durch eine Parallele ein Dreieck, ein Rechteck oder ein Trapez fest, dessen Flächeninhalt maximal sein soll. Sie bestimmen dazu jeweils die Parallelengleichung. Rotiert der Graph der verschobenen Exponentialfunktion, so entsteht ein Rotationskörper, an dem die Lernenden Volumenberechnungen durchführen. Spiegelt man den Graph der Exponentialfunktion mit eingeschränktem Definitionsbereich vertikal an einer Achse parallel zur y-Achse, so entsteht ein Querschnitt mit dem Aussehen eines Dammes. Diesen Querschnitt nutzen die Schülerinnen und Schüler als Modellierung.

Kompetenzprofil:

• Inhalt: Exponentialfunktion, Null- und Schnittstellen, Hochpunkt, rechtwinkliges bzw. gleichschenkliges Dreieck, Bestimmen von Parametern bei Extremwertproblemen (Strecke, Dreieck, Rechteck, Trapez), uneigentliches Integral, Transformation von Graphen (Verschiebung, Geradenspiegelung), Volumen Rotationskörper, Bestimmen einer Parabelgleichung, Tangente und Berührpunkt Prozentrechnung
• Medien: GTR/CAS, GeoGebra
• Kompetenzen: Probleme mathematisch lösen, mathematische Darstellungen
  verwenden, mit symbolischen, formalen und technischen Elementen der Mathematik umgehen