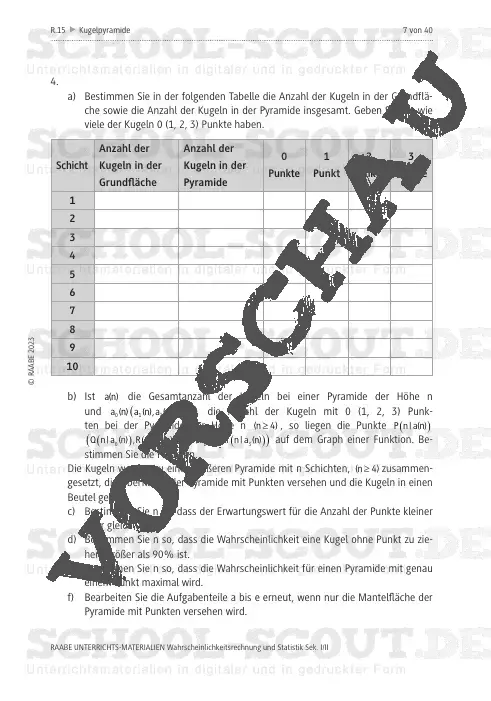
Pyramiden sind Schülerinnen und Schülern als geometrische Körper bzw. aus dem alltäglichen Leben bekannt. Setzt man eine Pyramide aus Kugeln zusammen und versieht die einzelnen Kugeln auf der Oberfläche (Mantelfläche) der Pyramide jeweils mit einem Punkt, so bieten die bepunkteten Kugeln die Grundlage für unterschiedliche Zufallsexperimente.

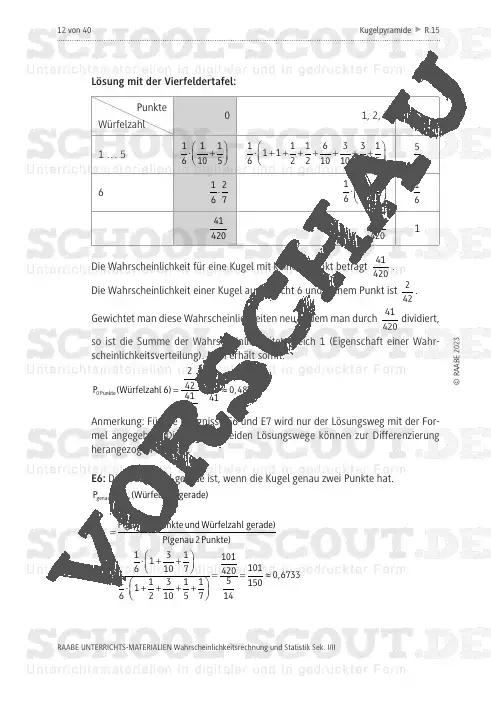
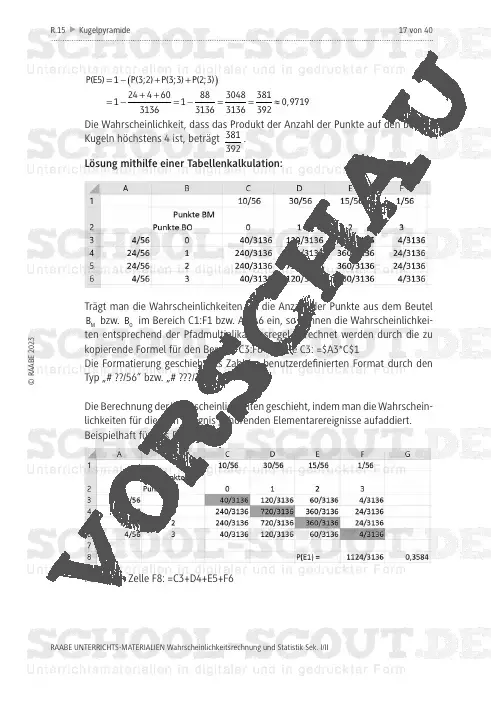
Zur Lösung der Aufgaben setzen die Jugendlichen (vereinfachte) Baumdiagramme, be-dingte Wahrscheinlichkeiten, die Binomialverteilung oder Sigma-Intervalle ein. Zudem überprüfen sie, ob zwei Ereignisse stochastisch abhängig oder unabhängig sind; sie testen Hypothesen und berechnen den Fehler 2. Art beim Hypothesentest.

Inhaltsverzeichnis:

• Hinweise
• M1 Beschreibung der Kugelpyramide
• M2 Aufgaben
• Lösungen

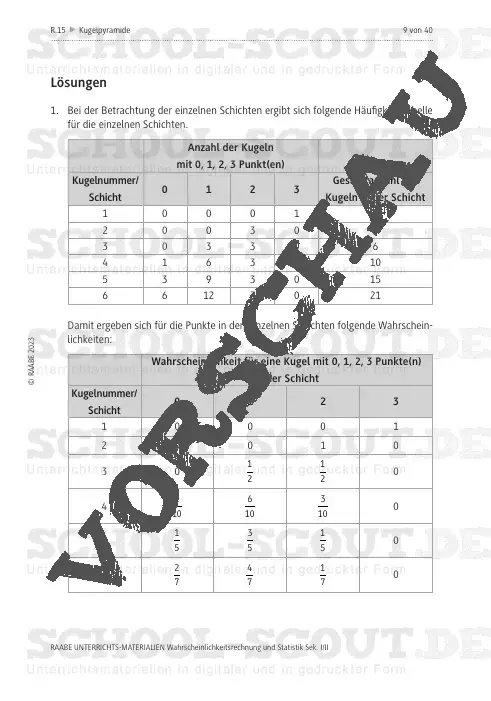
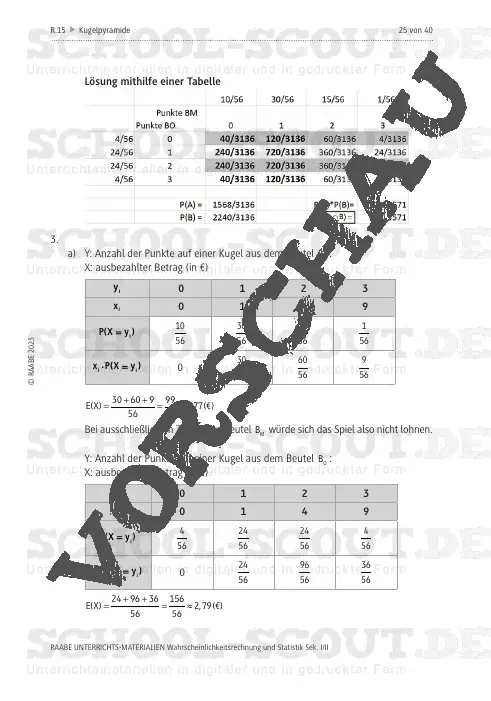
Die Schülerinnen und Schüler lernen: Ereigniswahrscheinlichkeiten mithilfe von teils komplexen Baumdiagrammen zu bestimmen. Die Lernenden festigen ihr Können und Wissen über die Bestimmung von (bedingten) Wahrscheinlichkeiten, indem sie für zugehörige Elementarereignisse die Wahrscheinlichkeiten auf unterschiedliche Arten bestimmen. Dies geschieht ebenso bei der Überprüfung auf stochastische (Un-)Abhängigkeit zweier Ereignisse. Die Jugendlichen berechnen Erwartungswerte und überprüfen, ob ein Spiel fair ist. Anhand der Binomialverteilung berechnen sie Wahrscheinlichkeiten, schätzen mithilfe der s -Regeln Anzahlen und überprüfen eine Hypothese.

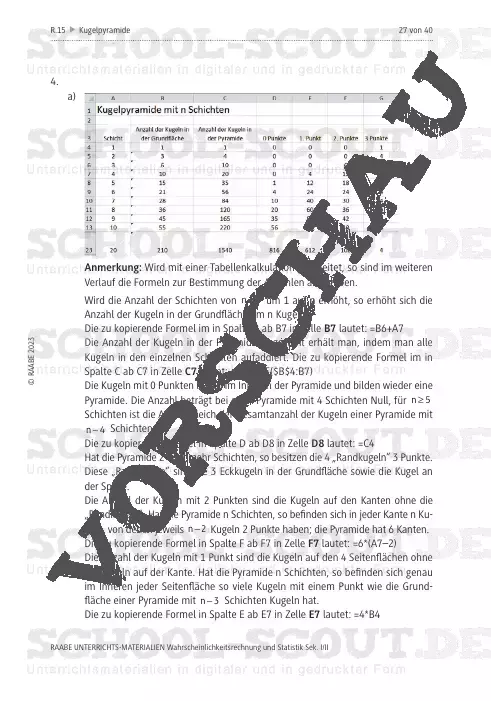
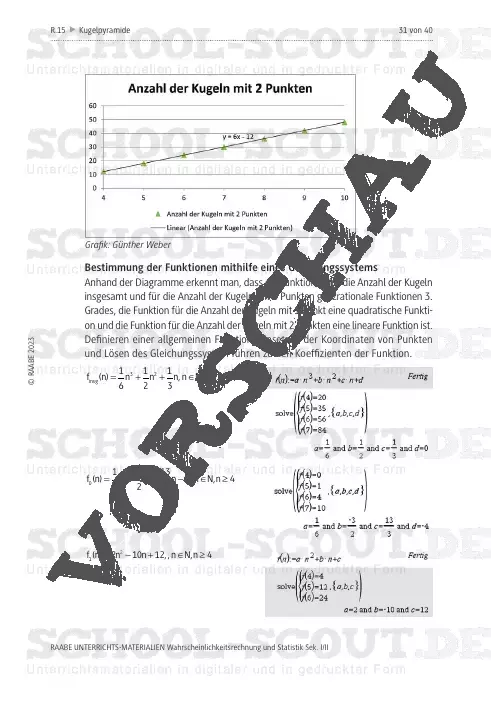
Für größere Kugelpyramiden leiten die Jugendlichen aus der Kugelanzahl Funktionen her. Mit diesen bestimmen sie die Höhe der Pyramide, sodass bestimmte Eigenschaften erfüllt sind.