Analysis: Matrjoschka
Eine Holzfigur als mathematisches Konstrukt
- Typ:
- Unterrichtseinheit
- Umfang:
- 31 Seiten (0,5 MB)
- Verlag:
- RAABE
- Auflage:
- 1 (2024)
- Fächer:
- Mathematik
- Klassen:
- 11-13
- Schulform:
- Gymnasium
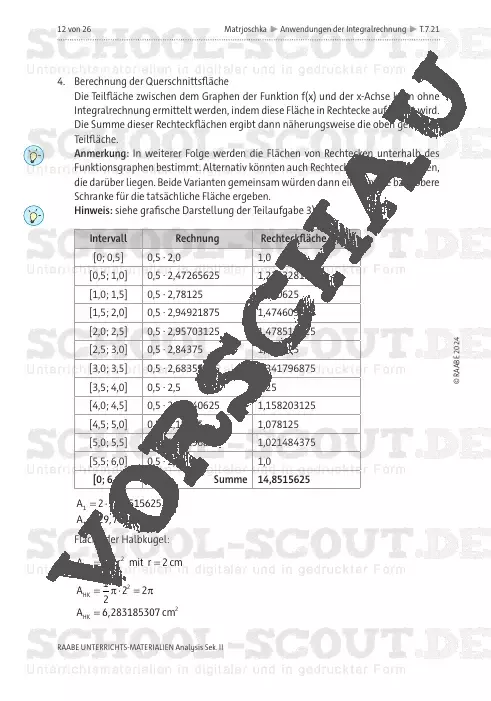
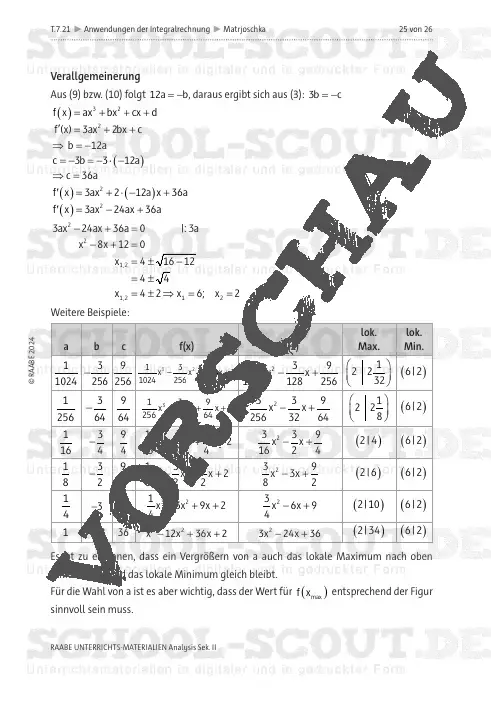
Die ineinander geschachtelten, hölzernen Figuren – Matrjoschkas – unterschiedlicher Größe sind für viele Touristen ein beliebtes Souvenir. Durch die geschwungene und gleichmäßige Form lassen sie sich aber auch mathematisch mit den Mitteln der Analysis beleuchten und berechnen.
Die Bearbeitung dieser Aufgaben kann der Motivation der Schülerinnen und Schüler dienen, sich mit der der Integralrechnung als Fortsetzung der Differentialrechnung zu beschäftigen. Dabei erkennen die Jugendlichen, dass die Integralrechnung verschiedene Aufgabenstellungen wesentlich vereinfacht, die andernfalls nur näherungsweise und mit erheblich größerem Aufwand zu lösen wären.
Dies ist beispielsweise bei folgenden Problemen der Fall:
- Berechnung der Bogenlänge nicht geradlinig verlaufender Funktionen
- Berechnung einer Fläche zwischen dem Graphen einer nicht geradlinig verlaufenden Funktion und der x-Achse
- Berechnung eines Volumens, das durch die Rotation einer nicht geradlinig verlaufenden Funktion um die x-Achse entsteht
Das Hauptziel der Aufgaben ist die Motivation. Alle anderen Lösungs- und Bearbeitungsschritte sind Neben- und Mitnahmeeffekte.
Die Schülerinnen und Schüler lernen:
Durch das anschauliche Beispiel der Matrjoschka-Puppe soll die Bearbeitung der Aufgaben motivierend wirken. Die Jugendlichen lösen Aufgaben sowohl mittels Näherungsverfahren als auch per Integration. Da letzteres einerseits die Genauigkeit der Ergebnisse erhöht und andererseits den Aufwand verringert, erkennen die Lernenden so die Notwendigkeit des Erwerbs neuer Kenntnisse, Fähigkeiten und Fertigkeiten.