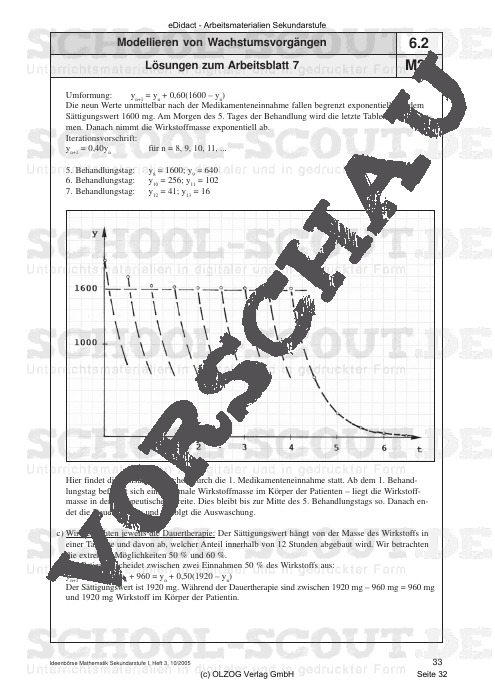
Modellieren von Wachstumsvorgängen
Kreative Ideenbörse Mathematik in der Sekundarstufe I
- Typ:
- Unterrichtseinheit
- Umfang:
- 34 Seiten (1,0 MB)
- Verlag:
- Mediengruppe Oberfranken
- Auflage:
- (2005)
- Fächer:
- Mathematik
- Klassen:
- 7-10
- Schulform:
- Gymnasium, Realschule
Diese Unterrichtseinheit handelt von deskriptiven mathematischen Modellen. Dabei geht es darum, ein Stück reale Welt vereinfacht und idealisiert mit mathematischen Mitteln zu beschreiben. Es geht nicht darum, im täglichen Leben vorgeschriebene Rechenverfahren zu benutzen, sondern angestrebt wird, ein komplexes Stück realer Welt durch etwas Gedachtes wenigstens näherungsweise zu erfassen. Zentrales Ziel ist, dass Schüler befähigt werden, mathematisches Modellieren angemessen zu bewerten. Dazu gehört nicht nur, Grenzen wahrzunehmen, sondern auch die Bedeutung dieses nicht nur in den Naturwissenschaften unverzichtbaren Verfahrens kennen zu lernen.
Ausgehend von einer Erfahrung mit einem Stück realer Welt kann ein mathematisches Modell aufgebaut werden, um damit zukünftige Entwicklungen zu berechnen. Nach korrekter Rechnung sind solche Prog-nosen im Modell wahr. Ob die Prognosen auch in der zukünftigen realen Situation gültig sind, ist noch offen. Dies muss zu gegebener Zeit eigens durch angemessene Beobachtungen geprüft werden. Stets muss im Blick bleiben:
- Es gibt die reale Welt.
- Es gibt Modelle von der Welt
Beim Arbeiten mit mathematischen Modellen genügt mathematisches Wissen allein nicht. Es bedarf unbedingt einer hinreichend subtilen Kenntnis des realen Sachverhaltes. Da es die knappe Unterrichtszeit nicht erlaubt, dass sich Schüler zuerst in ihnen fremde Sachzusammenhänge hinreichend einarbeiten, benötigen wir Beispiele aus alltäglichen außerschulischen Erfahrungsbereichen der Schüler. Dass dabei echte Daten benutzt werden, ist selbstverständlich.
Kompetenzen und Unterrichtsinhalte:
* Die Schüler erfahren, dass ein Modell eine vereinfachte Darstellung des Ablaufs eines realen Sachverhalts sein kann, die eine Untersuchung erleichtert oder erst ermöglicht.
* Sie erleben, dass ein mathematisches Modell nützlich sein kann, einen zwar bekannten, aber schwer durchschaubaren alltäglichen Sachverhalt besser zu verstehen.
* Sie erfahren, dass Modellrechnungen auch dazu benützt werden, Prognosen über zukünftige Ereignisse zu erstellen. Damit geeignete mathematische Modelle geschaffen werden können, sind zuerst tiefes Sachwissen und danach mathematische Kenntnisse unverzichtbar.
* Sie können bei der Bearbeitung der Aufgaben Metawissen erwerben: Was sind und was sollen Modelle leisten?